[Lecture Notes] ShanghaiTech CS181 Artificial Intelligence
Lecture 1. Intro
Three types of approaches
1. Symbolism 符号
Representing knowledge with: symbols and their compositions (expressions). 用离散符号的组合表示knowledge.
Inference and learning: manipulating symbols.
Advantages: expressive; interpretable; rigorous. 表达能力强; 可解释,人可读; 有严密数理逻辑基础
Disadvantages: hard to learn; rigid. 难以学习; 脆弱.
2. Connectionism 连接主义
Representing knowledge with: interconnected networks of simple units (e.g. neural networks). 用大量简单计算单元的加权连接 (典型:神经网络)
Inference: follow the computation specified by the network.
Learning: optimization of connection weights.
Advantages: good performance; flexible. 表现好; 灵活
Disadvantages: black-box; data-hungry; hard to incorporate knowledge. 黑盒,人不可读,不可解释; 需大量训练数据; 难以融入先验知识
3. Statistical Approaches 基于统计的方法
Representing knowledge with: probabilistic models.
Inference and learning: probabilistic inference.
Advantages: interpretable; rigorous; learnable. 可解释; 严密; 可学习.
Disadvantages: less expressive; less flexible. 表达能力不如符号; 灵活性不如连接主义.
Course Overview
- Search
- Constraint satisfaction problems
- Game
- Propositional logic
- First-order predicate logic
- Probabilistic graphical models
- Probabilistic temporal models
- Probabilistic logics
- Markov decision processes
- Reinforcement learning
- Machine learning
- Introduction to natural language processing
- Introduction to computer vision
Lecture 2. Search
Search Problems
A Search problem consists of:
- A state space
- A successor function
- A start state and a goal test
World state: every detail of the environment
Search state: only the details needed for planning
is the branching factor (maximum number of child nodes).
is the max depth.
is the depth of the shallowest solution.
Num of nodes:
Depth-First Search
Strategy: expand deepest node first.
Implementation: Fringe (a stack).
Time: if is finite
Space: (because only has siblings on path to root)
Not complete (unless we prevent cycles).
Not optimal.
Breadth-First Search
Strategy: expand shallowest node first.
Implementation: fringe (a queue).
Time: .
Space: .
Complete.
Optimal only if all costs are .
Iterative Deepening
Idea: get DFS’s space advantage with BFS’s time advantage.
Space:
Time:
Complete and optimal (unit cost).
Uniform Cost Search
Strategy: expand cheapest node first.
Implementation: fringe (a priority queue, priority = cumulative cost).
Complete and optimal, but slow.
Greedy Search
Strategy: expand a node with smallest heuristic (estimate of distance to goal)
Fast, but not optimal, not complete.
A* search
Combine UCS with Greedy.
Optimal when heuristic is admissable (heuristic cost actual cost).
时空复杂度不会比UCS差.
- admissible: 估计的cost小于实际cost
- consistent: 相邻节点的heuristic之差小于这两个节点的距离
Tree search: admissible 则最优
Graph search (避免重复visit): consistent 则最优
Lecture 3. Constraint Satisfaction Problems 约束满足问题
Two types of search problems
- Planning = standard search problems
- Identification = constraint satisfaction problems (CSPs)
Backtracking Search 回溯搜索
Backtracking = DFS + variable-ordering + fail-on-violation
Filtering: Forward checking
Keep track of domains for unassigned variables and cross off bad options.
Filtering: constraint propagation
Node consistency (1): Each node has valid value.
任何一个节点有可选值
Arc consistency (2): is consistent IFF for every in the tail there is some in the head which could be assigned without violating a constraint.
: 在X中随便选一个,Y仍然有得选
K-consistency: For each nodes, any consistent assignment to can be extended to the node.
对于任意个点,不论个点怎么选择,最后第个点都有得选
Strong k-consistency: also , , …, -consistent.
Claim: Strong n-consistency means we can solve without backtracking.
Ordering: MRV (Min Remaining Value 最少剩余值)
Also called Most constrainted variable
Choose the variable with fewest legal left values in its domain
优先选择最少剩余量的选项 (选可选颜色数最少的点涂色)
Ordering: LCV (Least Constraining Value 最少约束值)
Choose the least constraining value (variable that rules out the fewest values in the remaining values)
优先排除掉可能让邻居可选值最少的值,给相邻变量的赋值留下最大的灵活性
Tree-structured CSPs
Theorem: If the constraint graph has no loops, the CSP can be solved in time.
Algorithm:
- Order: parents precede children
- Remove backward:
for i in (n,2) removeInconsistent(Parent(Xi), i) - Assign forward:
for i in (1,n) assign Xi consistently with Parent(Xi)
Nearly tree-structured CSPs
Cutset conditioning ?
Lecture 4. Adversarial search
Concepts
Value of a state: best achievable outcome (utility) from that state 能获得的最好成绩
Minimax value: best achievable utility against an optimal adversary 对手最优时可能获得的最好成绩
Minimax search
Compute each nodes’s minimax value
Implementation:
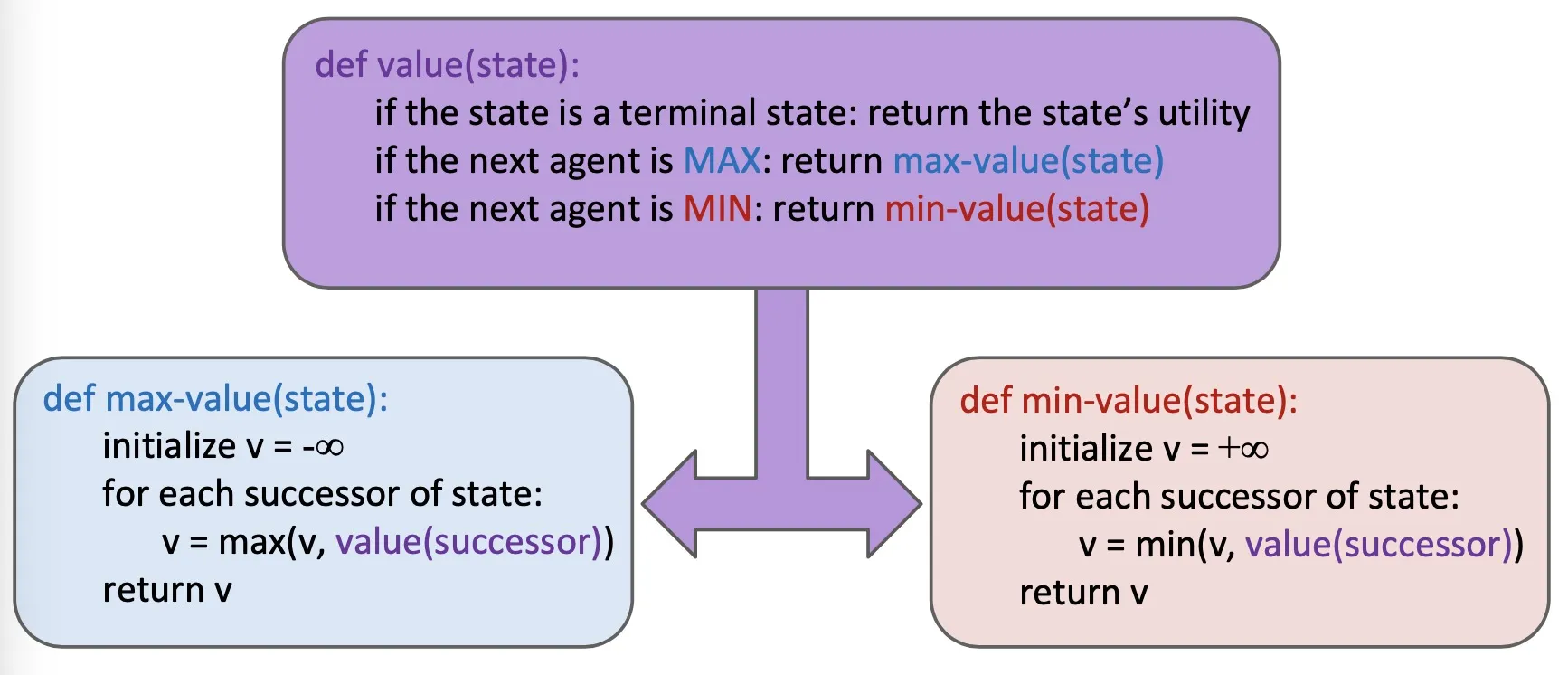
Efficiency:
Just like exhaustive DFS (相当于彻底的DFS搜索)
Time: , Space:
Depth-limited search (evalution functions)
Search a limited depth.
Replace terminal utilities with an evaluation function for non-terminal positions.
Ideal evalution function: actual minimax value of the state
Simple evalution function: weighted linear sum of features
Idea: limit branching factor by considering only good moves
Alpha-Beta pruning
Implementation
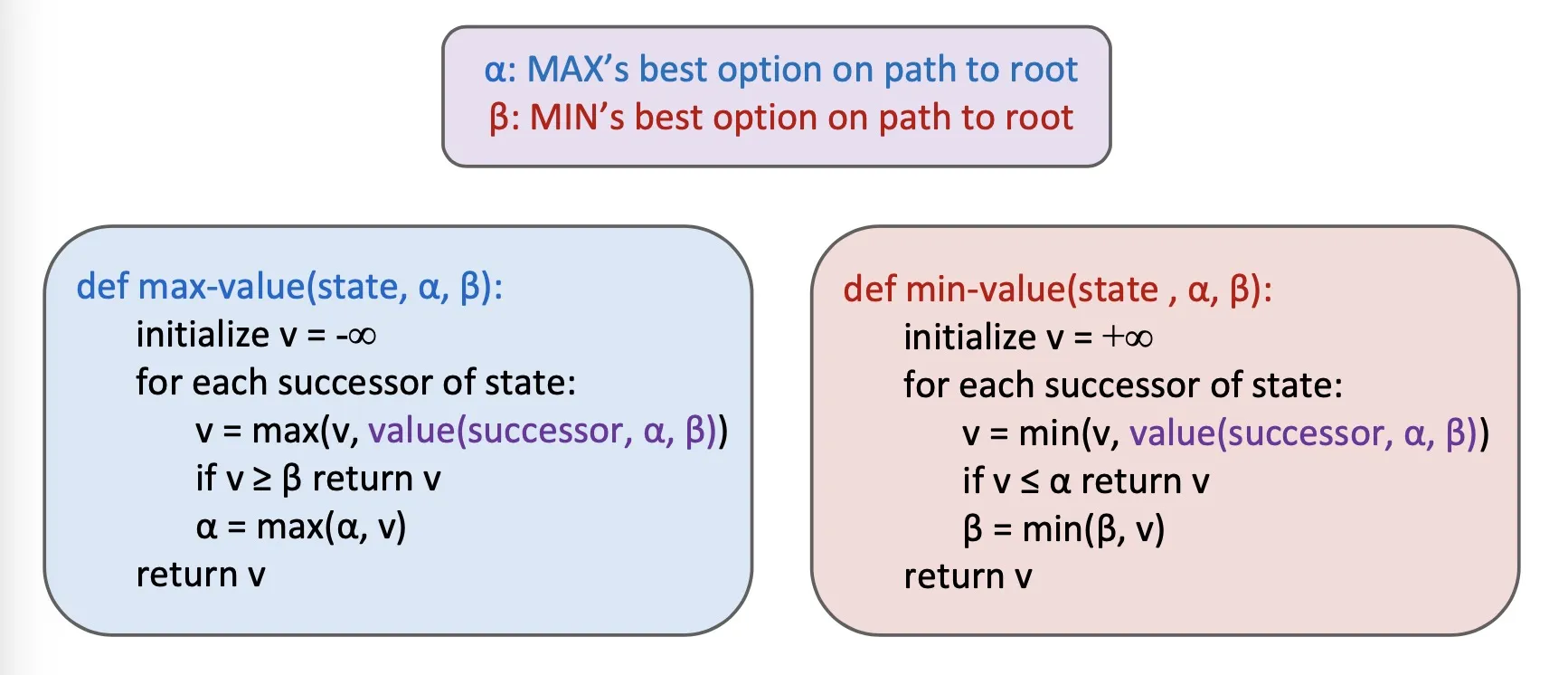
- pruning 受到展开顺序的影响
Expectimax Search
- Compute average score under optimal play (expected utilities = weighted avg of children)
Mixed layer types
- Enviroment is an extra agent.
- E.g. You, a random ghost, and an optimal ghost
Multi-Agent Utilities
- Multiple players. Each player takes care of only his utility.
Lecture 5. Propositional Logic
Logic-based Symbolic AI
Knowledge base
contains sentences representing knowledge
domain-specific
Inference engine
can answer questions by following the knowledge base
domain-independent
Formal Language
Components of a formal language:
- Syntax: 语法
- Semantics: 语义 specifies the sentences is true/false in each model
PL (propositional logic)
- Negation:
- Conjunction: (and)
- Disjunction: (or)
- Implication:
- Biconditional:
Logical equivalence

Validity and satisfiability
- valid: true in all models
- satisfiable: true in some models
- unsatisfiable: false in all models
Entailment
- In every world where is true, is also true.
- False entails everything.
Proof of entailment
A proof is a demonstration of entailment from to .
Method 1: model checking 模型检验
通过枚举所有可能得模型来检验。复杂度高。
Method 2: application of inference rules
- Search for a finite sequence of sentences each of which is an axiom or follows from preceding sentences by a rule of inference
- axiom: 公理 a sentence known to be true
- rule of inference: a function that takes one or more sentences (premises) and returns a sentence (conclusion)
- Sound inference: 能证明出来的一定是entailed的
- Complete inference: entailed的一定能被证明出来
- 对于 Horn logic, Resolution 是 sound 和 complete 的
- Search for a finite sequence of sentences each of which is an axiom or follows from preceding sentences by a rule of inference
CNF (conjunctive normal form)
conjunction of disjunctions of literals (clauses)
- literal: a simple symbol or its negation: or
- clause: disjunction of literals :
- CNF: conjunction of literals:
conversion to CNF
- 1: 把 换成
- 2: 把 换成
- 3: 把 换成 ; 换成
- 4: 用分配律 ( over )
Resolution
为了证明 , 我们去证明 unsatisfiable.
Step 1. Start from
Step 2. Build a set of sub-formulas
- Write in CNF (写成 形式)
- Let
Step 3. 对 做 resolution:
注: 不能说
Reach an empty clause
Horn Logic
普通 propositional logic 的 Inference 通常NPC复杂.
Horn logic 用 forward / backward chaining 可实现线性复杂度.
形式: 或
Modus Ponens (MP规则): 所有前提fixed, 则结论 fixed
Forward chaining: 从facts入手, 加入新fact直到得到query
Backward chaining: 从query入手, 为证明query找前提条件
Forward chaining 对于 PL, FOL, Horn Logic 都是 sound 和 complete 的.
Backward chaining 对于 PL, FOL 是 sound 但 incomplete 的, 对于Horn是complete的.
Lecture 7. Bayesian Networks
概率
条件概率:
Bayes rule:
Chain rule:
Syntax
贝叶斯网络语法:
- DAG (directed, acyclic graph) 有向无环图
- CPT (conditional probability table)
- CPT for each node given its parents (每个节点存有 给定父节点的条件概率分布)
Semantics
Global semantics
所有CPT相乘
Conditional independence semantics
给定父节点, 则该节点与非子孙节点独立
Independence 符号
Markov blanket
Markov blanket consists of parents, children, children’s other parents (父,子,配偶)
Every variable is conditionally independent of all other variables given its Markov blanket.
给定markov blanket, 与所有其它变量条件独立
Common cause: 给定父节点(cause), 两个child(effects)独立
Common effect: 给定子节点(effect), 两个父节点(cause)不独立 (v-structure)
D-separation
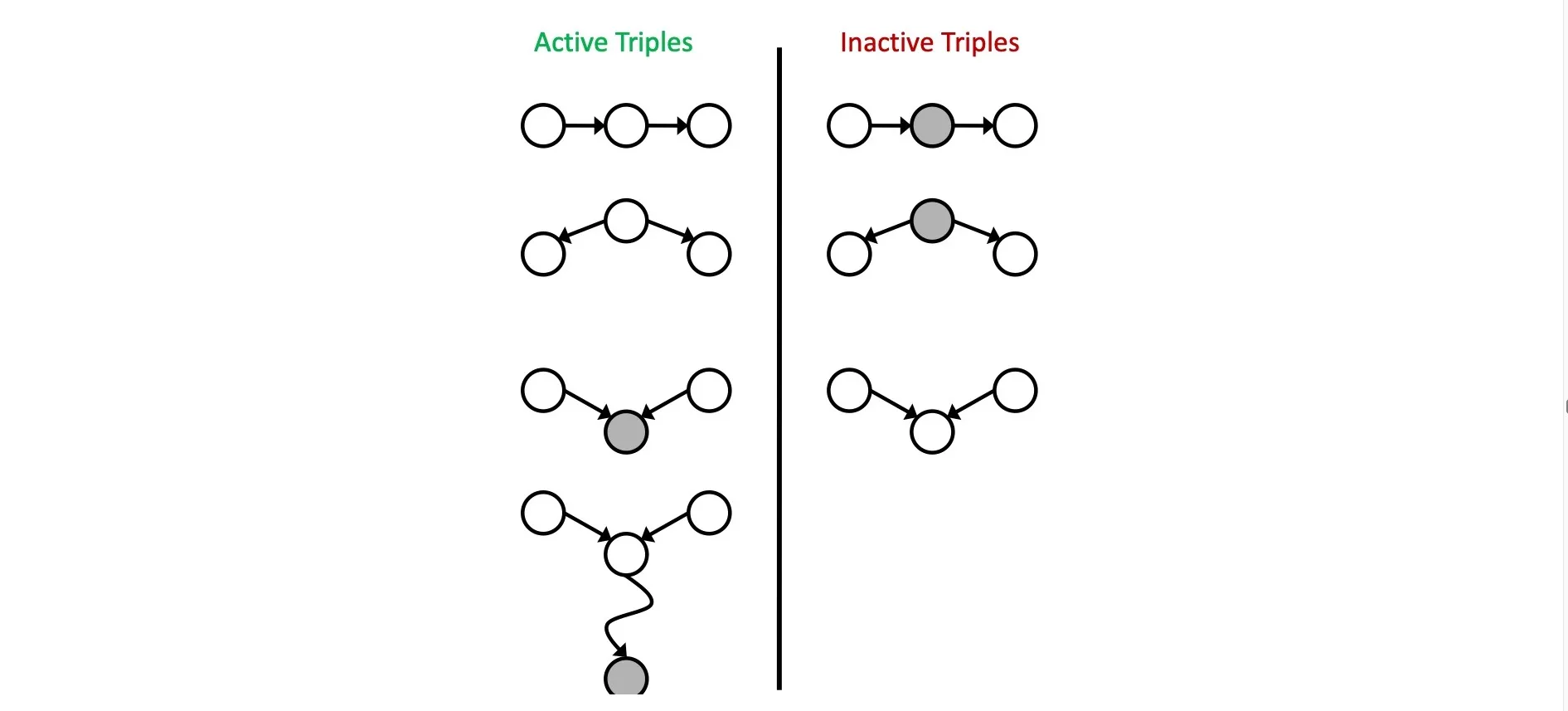
If all paths from X to Y are blocked (at least 1 inactive triple), then X is d-separated from Y by Z ()
Markov networks
undirected graph(无向图+clique全相连子图) + potentials 势函数(为每个clique的打分, 未经normalize, 不是概率)
Undirected graph + potential functions
- Undirected graph 无向图
- For each clique or max clique, a potential function is defined
联合概率 正比于 势函数乘积
is the potential over clique
is the normalization coefficient (partition function)
Conditional Independence in Markov networks
要判断, 只需判断从A到B的所有path是否都被C挡住了
Markov blanket
Markov blanket 就是这个节点的所有neighbor
Bayesian networks inference
Exact inference
Inference by enumeration
CPT相乘得联合概率, sum out 掉 hidden variables
- Evidence variables:
- Query variable: (我们想求: 给定时的条件概率, 即 )
- Hidden variables:
Steps:
Select the entries consistent with the evidence
Sum out to get joint distribution of and
Normalize
Variable elimination
对每个 hidden variable 做 join and eliminate
指数复杂度, 但当贝叶斯网络为 poly tree 时, 为线性复杂度
Efficient inference on polytrees
Approximate Inference
Prior sampling
自顶向下采样
Rejection sampling
当采样与evidence不一致时丢弃
Likelihood weighting
只对non-evidence采样, 为每个样本计算weight (weight为所有evidence var条件概率的乘积)
Gibbs sampling
顺序采样, 每个样本由之前样本修改而来, 得到序列
Lecture 12. Probabilistic temporal models
Markov models
(Assume discrete variables that share the same finite domain).
Values in the domain is called states.
The transition model specifies how the state evolves over time.
Stationarity assumption: same transition probabilities at all time steps.
Markov assumption: 给定, 与 条件独立
- 给定现在,过去与未来独立
- 每个时间点只与前一个有关
- First-order Markov Model
A k-th order model allows dependencies on earlier steps
Joint distribution:
Markov models 是不是 Bayes nets 的特例? Yes and No.
- Yes: 有向无环图, 联合概率 = 条件概率乘积
- No: 无限多变量, 重复的transition model 不符合 标准Bayes net syntax.
Forward algorithm
Given initial distribution
递归更新
对于大多数markov chain, 最初的分布带来的影响越来越小, converge到的 stationary distribution 与最初分布无关.
Stationary distribution:
Hidden markov models (HMM)
Only observe evidence . Underlying markov chain over states .
An HMM is defined by
- Initial distribution
- Transition model
- Emission model
Joint distribution
Notation:
Filtering
给定所有evidence, 计算当前state的值的概率
Infer current state given all evidence:
May skip normalization .
每一步的复杂度是 , 其中 是state数量
Most likely explanation
The product of weights on a path is proportional to that state sequence’s probability.
Viterbi algorithm
For each state at time , keep track of (unnormalized) maximum probability of any path to it.
时间空间复杂度与 forward algorithm 相同.
Dynamic Bayes Nets (DBNs)
每个 HMM 都是 DBN.
每个 discrete DBN 都能用 HMM 表示.
每个 HMM state 都是 DBN state variables 的 Cartesian product.
Particle Filtering
Exact inference: variable elimination
Approximate inference by particle filtering
- Initially draw particles, each has weight 1
- Propagate forward: 根据 transition model 移动 particles
- Observe: 根据 emission model 给每个 particle 加上权重
- Resample: Draw N particles from the weighted sample distribution. 对加权后的sample重新采样, 采到的概率根据权重而定
如果没有 resample 这一步,那么 particle filtering 与 likelihood weighting 近似
Lecture 13. Markov decision processes
MDP
An MDP is defined by
- State
- Actions
- Transition function or
- Reward function and discount
- Start state, terminal state
MDPs are non-deterministic search problems.
(In deterministic single-agent search problems, we want a plan, a sequence of actions)
For MDPs, we want an optimal policy
utility: sum of rewards
得到了MDP的policy之后,MDP表现得像关于policy的markov chain
Optimal quantities
value / utility of a state
is the expected utility starting in and acting optimally
value / utility of a q-state
= expected utility starting out having taken action from state and thereafter acting optimally
Bellman equation
Value of states (recursive definition)
Bellman equation
Value iteration
Time limited values: 是如果 步之内结束, 的最佳值
Value iteration
Starting with
Policy extraction (单步 expectimax)
每一次迭代的复杂度: , 是state数量, 是action数量
Theorem: 一定会收敛到唯一的最佳值 converges to unique optimal.
Q-value iteration
Starting with
Policy extraction
Policy iteration
Step 1: Policy evaluation
Calculate utilities for some fixed (not optimal) policy
Start with
Given , calculate
Repeat until convergence
Step 2: Policy improvement
Update policy using one-step look-ahead with resulting converged (not optimal) utilities as future values.
One-step look-ahead
Repeat until policy converges.
policy iteration 第一步的复杂度是 per iteration, 总复杂度是
Policy iteration is still optimal, can converge much faster under some conditions. (policy iteration 不一定比 value iteration 快 [2019 Fall Final])
Lecture 14. Reinforcement Learning
Model based learning
Learn an approximate model based on experiences.
Solve for values as if the learned model is correct.
Step 1. Learn empirical MDP model
- 对于每个 记住(当前state, 采取action之后的结果 )
- Normalize 学习出 transition model
- 遇到 时记下 reward
Step 2. Solve the learned MDP
- e.g. Use value iteration
Passive reinforcement learning
给定固定的 policy , 但不知道 , .
Execute the policy and learn from experience to get state values.
Direct evaluation: 直接估计未来 reward 之和, 不记录 transition model
- 按照给定的 policy 去做
- 每次访问一个 state 时, 记下 sum of discounted rewards
- 取平均
Direct evaluation 好处:
- Easy to understand
- Does not require knowledge of ,
- Can compute correct average values using just state transitions
缺点
- Wastes information about state connections
- Each state must be learned separately
- Take a long time to learn
Sample-based policy evaluation
此处不知道T和R, 所以采用sample的方式
Temporal Difference Learning
Idea: update each time we experience a transition
Sample of is
Update:
(越新的sample越重要, forget about the past)
Q-learning
Sample-based Q-value iteration
Sample is
Update new estimate
Approximate Q-learning
当state太大的时候,用feature的加权求和代表state.
Approximate Q-learning 属于 model-free learning. [2019 Fall Final]
Reinforcement learning
MDP without knowing T and R
Offline planning VS online learning
Model based learning
Model free learning
Policy evaluation: Temporal Difference Learning
Exponential moving average
Computing q-values / policy: Q-learning
Exploration vs exploitation
random exploration, exploration function
Approximate Q-learning
Feature-based representation of states
Lecture 15. Supervised machine learning
Supervised learning
- Input: 有标注的训练集 ,
- Output: 尽可能接近 target function 的函数 (hypothesis)
Supervised learning 的类型
- Classification: 离散输出
- Regression: real-valued 输出
- Structured: structured 输出
Naive bayes classifer
Naive bayes model:
所做的假设: 给定label , 所有features独立
总参数与呈线性关系
Bag-of-words naive bayes
Features: is the word at position
Each word is identically distributed.
All positions share the same conditional probabilities . 所有位置CPT相同
Called ‘bag-of-words’ because model is insensitive to word order or reordering.
Inference for naive bayes
Goal:
Step1. Get joint probability of label and evidence for each label
将所有CPT相乘
Step2. Normalization
Maximum likelihood estimation
empirical rate (frequency of seeing this outcome)
Using empirical rate will overfit the training data.
Important concepts
Learn parameters (e.g. model probabilities) on training set
Tune hyperparameters on held-out set
Compute accuracy of test set
Overfitting: learn to fit the training data very closely, but fit the test data poorly
Generalization: try to fit the test data as well
过拟合产生的原因
- 训练集不能代表真实的数据分布
- 训练集太少 或 训练集噪声太多
- 太多attributes, 部分属性与分类任务无关
- 模型过于 expressive
避免overfitting
- 更多训练集
- 去除无关属性
- 使用正则化、提前停止、pruning等手段限制模型的expressiveness
Laplace smoothing
Laplace’s estimate: pretend you saw every outcome k extra times
Linear classifiers (perceptrons)
Inputs are feature values. Each feature has a weight.
Sum is the activation.
Output +1 if , -1 otherwise
训练(更新):
Lecture 16. Unsupervised machine learning
Clustering
K-means
Voronoi diagram: partitions the space by nearest cluster center
Consider the total distance to the means

Two stages
- fix means c, update assignments a
- fix assignments a, update means c
EM
EM can be used to learn any model with hidden variables (missing data). [Fall 2019 Final]
E-step: Assign data instances proportionately to different models 计算每个数据点属于不同cluster的可能性分布
M-step: Revise each cluster model based on its proportionately assigned points. 更新cluster的分布
GMM (Gaussian mixture model / mixture of Gaussians)
当使用EM学习GMM时, M-step计算的是weighted maximum likelihood estimation (MLE).
当 all the Gaussians are spherical and have identical weights and covariances, with hard assignments 的时候, EM降级成k-means
Lecture 16. NLP 自然语言处理
Constituency Parsing
Constituent parse tree (phrase structure)
每个中间的节点代表一个 phrase / constituent
Grammar: the set of constituents and the rules that govern how they combine
Context-free grammars (CFGs) (phrase structure grammars) 四个组成部分
- A set of terminals (words)
- A set of nonterminals (phrases)
- A start symbol
- A set of production rules (specifies how a nonterminal can produce a string of terminals and/or nonterminals)
Dependency grammar: focus on binary relations among words. (CFG focus on constituents)
Sentence generation
- 使用grammar生成string
- 从仅有 start symbol 开始, 递归地使用rules重写句子直到只剩下 terminals
Sentence Parsing
- Taking a string and grammar, return one or more parse trees for that string
- Probabilistic grammars (stochastic grammars): 每条规则具有概率, parse tree的概率是使用过的每条规则的概率之积
- Ambiguity: 如果一句话有两个或以上的可能得parse tree, 则 ambiguous
Parsing algorithm
A brute-force approach
- Enumerate all parse trees consistent with the input string
- Problem: # of binary trees with leaves is (exponential growth)
CYK algorithm
A bottom-up dynamic programming algorithm
Applies to CFG in Chomsky Normal Form (CNF)
- 仅两种production rules: A → BC 和 A → w
- 任何CFG都能转化为CNF
- Probabilistic CFGs tend to assign larger probabilities to smaller parse trees. [Fall 2019 Final]
Build a table so that a non-terminal A spanning from i to j is placed in [i-1, j]
S (span整个string) 应该位于 [0, n]
Base case: 如果有一条规则 ,则 应该在 [i-1, i] 的位置
Recursion: 如果 , 在 [i,k], 在 [k, j], 则 在 [i, j]

- Probabilistic parsing: 在运行CYK算法的时候,在 [i-1, j] 时,对于每个中间节点A添上最可能的由A出发覆盖 [i,j] substring 的parse tree的概率
Dependency Parsing
- A dependency parse is a directed tree where
- nodes are the words in a sentence (ROOT 是一个特殊的根节点)
- links between words represent their dependency relations
Lecture 18. Final Review
That’s all!