KMP算法 字符串匹配
Leetcode 28 题目描述
链接:leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string
28. 找出字符串中第一个匹配项的下标
给你两个字符串
haystack和needle,请你在haystack字符串中找出needle字符串的第一个匹配项的下标(下标从 0 开始)。如果needle不是haystack的一部分,则返回-1。示例 1:
2
3
4输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。示例 2:
2
3输入:haystack = "leetcode", needle = "leeto"
输出:-1
解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
朴素解法一行 复杂度
1 | |
或者把这一行中的 std::string::find 手写一遍
1 | |
这种朴素方法能过但最坏时间复杂度是 ,如下面的例子
1 | |
使用KMP算法能把复杂度降至 。
KMP算法 复杂度
KMP是Knuth-Morris-Pratt,三个人名。
为了解释为什么KMP算法更快,我们需要先考虑一下朴素算法会怎么做。
举一个例子:haystack(原串,原字符串,主串)为 abeababeabf, needle(匹配串,模式串)为 abeabf。
朴素算法的问题
先考虑一下朴素算法会怎么做:
1 | |
原串和匹配串各有一个指针(代码块中竖线 "|" 代表指针),最初两个指针都指向各自的起始字符 "a"。
起始字符 "a" 之后的字符 "b" "e" "a" "b" 都是匹配的,两个指针会同时向右移动。
1 | |
下一个字符应该是 "f",但原串中下一个字符是 "a",对不上了!此时原串中的指针会移动至起始点的下一个位置,即第二个字符 "b" 处,而匹配串中的指针会移动至起始点,如下图所示:
1 | |
KMP匹配过程
发现效率问题了吗?
我们要找"abeabf",现在已经找到"abeab" 了,因为最后一个字符匹配不对而前功尽弃。
但是我们没必要前功尽弃。注意到 "abeab" 中有一个相同的“前缀”和“后缀” "ab",我们可以将原串中的指针移动到第二个 "ab" 处。
1 | |
这样的话,我们不需要推倒重来从"a"重新找,而是可以从 "ab" 继续找。更具一般性地说:我们不需要回到匹配串的起始位置,而是根据相同的“前缀”和“后缀”,移动到这个**“前缀”下一个出现的位置继续匹配**。
这就是KMP算法的匹配过程。
最长相同前后缀 (next数组)
现在我们就明白了为什么KMP算法比朴素解法更快。
KMP能够利用已经匹配的原串部分相同的“前缀”和“后缀”来加速下一次匹配(不需从头匹配,而是回到前缀第二次出现处即可)。
但是有一个问题,我们如何找出上面这个“前缀第二次出现的位置”,或者说,如何找出当前已匹配字符串部分的最长前缀和后缀?
KMP算法引入了一个next[] 数组。next[i] 表示匹配串中前i**个字符组成的子串最长的相同前缀后缀的长度**。
定义:前缀、后缀不能是整个字符串。
例如 "abcd" 前缀包含 “a”, “ab”, “abc”,而不包括 “abcd”。
例如 "abcd" 后缀包含 “d”, “cd”, “bcd”,而不包括 “abcd”。
再例如 "a" 没有前缀。空字符串 "" 也没有前缀。
举上面一个例子,字符串 "abeabf" 的 next[] 数组值应为[0,0,0,1,2,0]。
next[0] = 0,因为 "a" 没有相同前后缀
next[1] = 0,因为 "ab" 没有相同前后缀
next[2] = 0,因为 "abe" 没有相同前后缀
next[3] = 1,因为 "abea" 最长相同前后缀为 "a"
next[4] = 2,因为 "abeab" 最长相同前后缀为 "ab"
next[5] = 0,因为 "abeabf" 没有相同前后缀
那么还是上面的问题,怎么求 next 数组?暴力解法为 ,但KMP算法有一个 的求法。
首先 next[0] = 0。假设现在我们已经计算出了 next[j] = i,即下图中两个浅蓝色区域①和②是相同的前后缀部分。
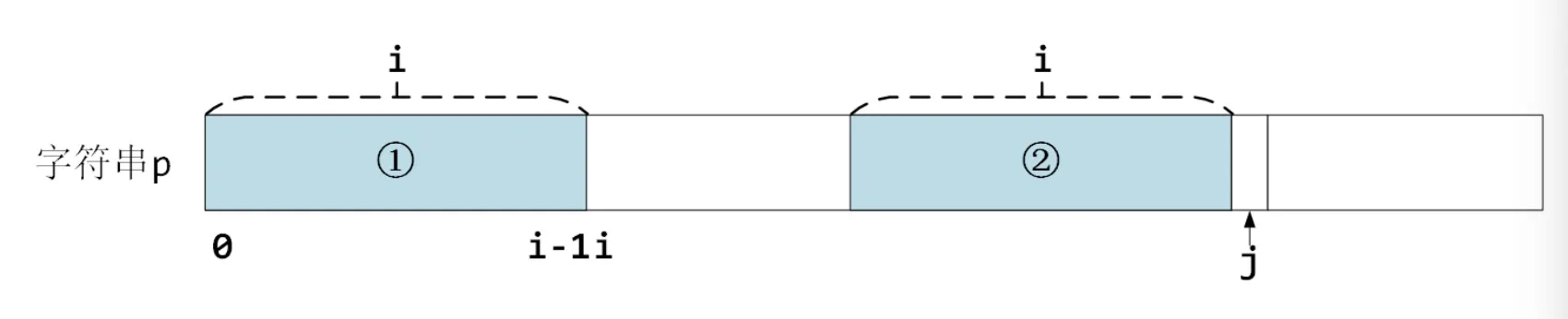
那么j++ 后计算 next[j+1] 时:
如果说新的一个字符相等,那么简单了,前后缀各多一个字符(深蓝色部分),那么 next[j] = i+1,如下图所示。

如果说不相等(褐色部分与深蓝色部分),那么必然不能像刚才一样直接在i后+1了。我们需要找一个新的最长公共前后缀,即下图中,在区域①中找最长前缀③,在区域②中找相等的最长的后缀④。
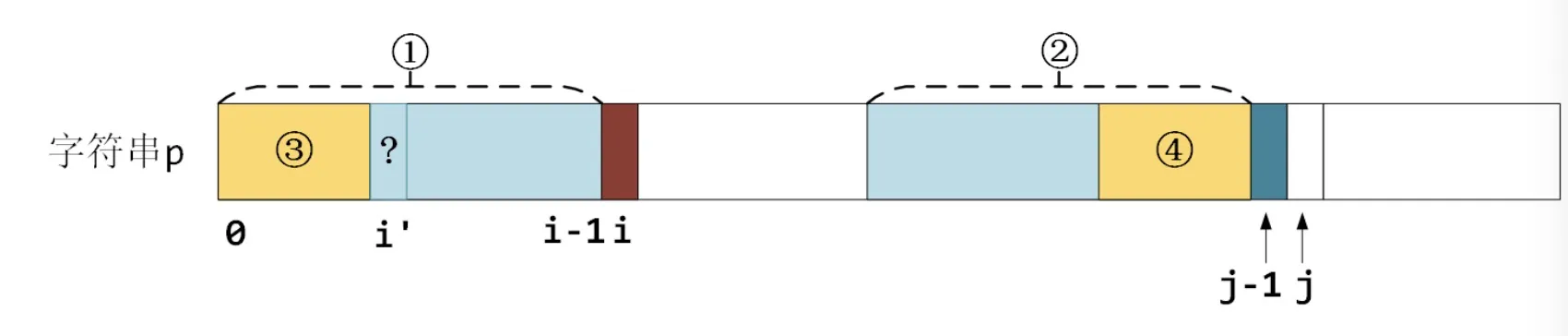
给上图举个例子吧。考虑字符串 "aabxyzagggaabxyzaa",目前已经查找到最长前后缀为 "aabxyza"。现在新的字符 "g"(褐色) 和 "a"(深蓝色) 不相等了,那么需要找区域③和区域④,如下图黄色框所示。

怎么找③和④呢?
注意到,①和②本身是完全相等的,因此,我们可以将 “在①中找最长前缀③,在②中找相等的最长后缀④” 的问题转化为 “在①中找最长前缀③,和一个相等的最长后缀④”,如下图所示
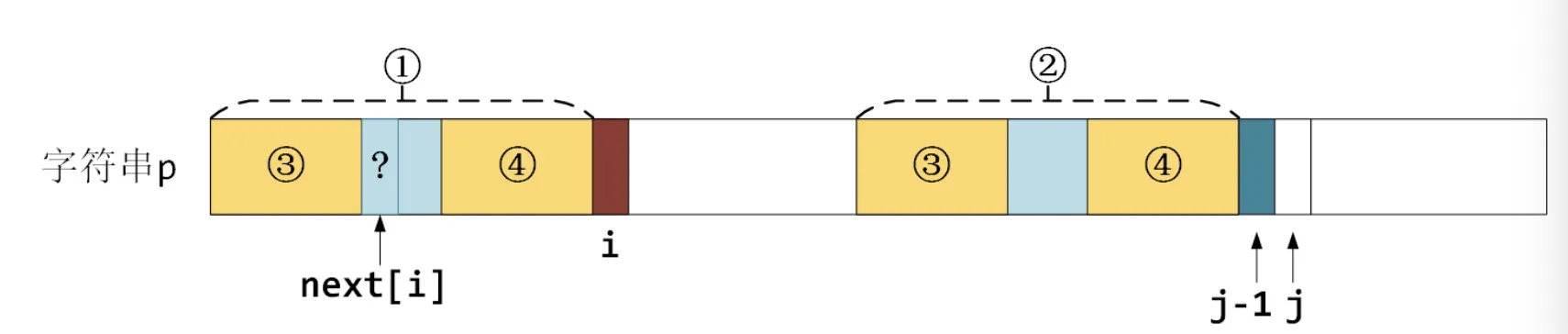
这不就是子串①的最长公共前后缀的定义吗?而这个①的最长公共前后缀已经求出来过了,值就是 next[i] (因为i < j,我们遍历到 j 时 next[i] 已经计算出来过了。
那么我们直接查找一下 next[i],然后判断一下 p[next[i]] (上图中问号?所在处) 和 p[j](图中深蓝色部分) 是否相等即可。如果不相等,让 i = next[i] 继续重复上述过程。
如果一直匹配失败,最终 i 会等于0,停到字符串第一个字符 p[0] 的位置。
next[] 数组求解代码:
1 | |
next求解完成之后的匹配过程
计算完 next 数组后,我们可以回到字符串的匹配过程了。
上面我们说过,匹配失败的时候,我们不需要从头开始,而是移动到这个“前缀”下一个出现的位置继续匹配。这里我们就可以利用刚刚算好的 next 数组,查找“前缀”下一个出现的位置。
在代码中我们仍然定义两个指针 i 和 j,分别是原串和匹配串的指针。
如果匹配失败,则将匹配串指针 j 移动至 next[j] 的位置。
代码如下:
1 | |
完整代码
1 | |
参考题解: